中学最初の方の理科の問題【密度や濃度】で理科という科目が嫌いになったりしていませんか?「計算問題もあって意味がよくわからない」「何か濃度と聞いただけで嫌になってしまう」そんな声を時々耳にします。
今回は苦手分野から得意分野になれるよう「濃度」について解説をしたいと思います
それではまいります。
質量パーセント濃度って何?
難しい言葉に聞こえると思いますが、全く気にしなくていいです。 要するに「濃度」と理解して問題ありません。
濃度とは簡単にいいますと溶液などに含まれる成分量の割合のことですが、いまいちピンときませんね。濃度という言葉をまずはイメージできるようにしましょう。
具体的なわかりやすい例として「食塩水」や「砂糖水」がありますね。
食塩水の濃度:食塩水に含まれる食塩の量の割合
割合が高ければ濃い(しょっぱい)ですし、割合が低ければ薄い(塩の味があまりしない)という感じです。
砂糖水の濃度:砂糖水に含まれる砂糖の量の割合
割合が高ければ濃い(甘い)ですし、割合が低ければ薄い(甘くなく水だけの味しかしない)となります。
濃度のイメージ 掴めましたでしょうか?
問題文に出てくる単語の意味を理解しよう
問題に入る前に文章に出てくる単語の意味を覚えましょう。
この単語の意味を勘違いしている場合が実はけっこうあるんです。いくら濃度の公式がわかっていて、計算問題をクリアできたとしてもスタートラインで勘違いをしていてはとてももったいないですし答えも当然違います。
主には以下の3つです。
- 溶質:液体の中に混ざって溶けている物質
- 溶媒:物質を溶かしている液体
- 溶液:溶けた物質+物質を溶かしている液体(要するに全部のこと)
うーん、何となくはわかったけど、あまり聞きなれない言葉だし・・・というか感じですよね?
さきほどの「食塩水」「砂糖水」を例に具体的に説明しましょう。
「食塩水」の場合
- 溶質:食塩(しお)
- 溶媒:水(みず)
- 溶液:食塩水(しおみず)
「砂糖水」
- 溶質:砂糖(さとう)
- 溶媒:水(みず)
- 溶液:砂糖水(さとうみず)
具体的にイメージ掴めましたね?
公式を簡単に理解しよう
濃度の公式は以下です。

暗記するのは好ましくありませんが、把握はしておいてください。これを先ほどの塩・水・食塩水で表してみます。
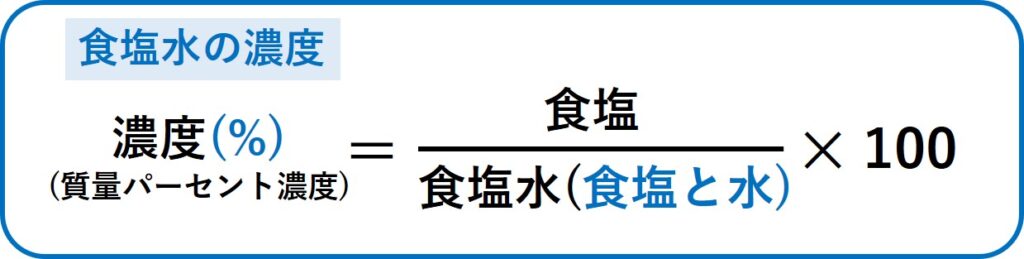
こうするとわかりやすいですね。
つまり、混ざっているもの(食塩や砂糖)を全部で割ったら濃度になるということです。
塩を食塩水で割って×100したら濃度(全体に対する塩の濃さ)が出るという意味です。
念のため補足ですが ×100 というのは大丈夫でしょうか?割った答えが 0.3なら0.3×100で30%、0.05なら×100で5% ということです。
さあ、問題を解いてみよう!
1~2基本問題、3~4普通、5~6は難しい問題です。

準備と注意事項:全体(食塩水)を出すことを忘れずに!水で割ったらダメですよ。
計算式:5g ÷ (5g+20g) × 100 = 20%
答え:20%

準備と注意事項:12%は計算上はそのまま使えないので0.12とすること
計算式:50g × 0.12 = 6g
答え:6g

準備と注意事項:問題2の食塩水を整理する(食塩6g、水は50-6=44g、食塩水は50g)
計算式:6g ÷ (50g+100g) × 100 = 4%
答え:4%

準備と注意事項:食塩は 150g × 0.08 = 12g
計算式:12g ÷ 0.03 = 400g , 400g – 150g = 250g
答え:250g

準備と注意事項:水の量を問われていることに注意する(全体の食塩水ではない)
計算式:18g ÷ 0.05 = 360g , 360g – 18g = 342g
答え:342g

準備と注意事項:考え方は複数ありますが、濃度は塩の比率です ということは残りが水の比率(100%-15%=85%)となりますね
計算式:食塩水=425g ÷ 0.85 = 500g , 食塩=500g – 425g = 75g
答え:75g
まとめ
いかがでしょうか?
最後まで読んでくれてありがとうございました。 これを読んだくれた方が「濃度」が得意になった!と感じてくれていると嬉しいです。

補足:困った時のおすすめ
数学や理科などには特に言えることですが、何か困ったときやよくわからなくなった時は
- 「何か具体的な身近なものに置き換えてみる」
- 「簡単なことに置き換えてみる」
- 「図や絵を書いてみる」
これを意識してみるといいですよ。
参考:密度の問題解説はこちらから






コメント