今回は「溶解度・溶解度曲線」について解説します。言葉の意味をきちんと理解することと、後から出てくる溶解度曲線に関係する表やグラフを読み取れるようになればきっと大丈夫です。この分野で苦手にならないようにわかりやすく解説していきたいと思います。
溶解度とは?
食塩を水に溶かす時の例で説明しましょう。
100gの水を用意して食塩を水に少しずつ加えながらかき混ぜて溶かしていきます。ずっと続けていくと「もうこれ以上食塩を足しても全然溶けない!」ってなりますよね。
その溶ける限界の量が溶解度です。(この場合は食塩の溶解度ですね)
水100gにきちんと溶けてくれる物質の質量(溶ける最大量)=溶解度
飽和水溶液とは?
「これ以上もう溶けない!」ぎりぎりの一番濃い状態の水溶液のことです。先ほどの食塩水の例をあげると「100gの水に食塩を足し続けてもう溶けなくなった時の食塩水」が飽和水溶液です。
限界まで物質を溶しかした水溶液=飽和水溶液
溶解度曲線とは?
さあ、溶解度曲線について説明していきましょう。その前に下の表をご覧ください。

3種類の物質の溶解度(100gの水に溶ける質量)の比較を表したものですが、もう1つ軸があります。
それが「温度」です。
表にあるように物質は水を熱して温度を上げていくと溶ける量は増えていきます。この点をまず覚えておいてください。
水の温度が上がる=物質の溶ける質量は増える
ただ、物質によって溶ける質量には「差」があって温度が上がれば上がるほどどんどん溶ける物質もあれば、温度をいくら上げてもほんの少しずつしか溶ける質量が増えていかない物質もあります。
その温度と物質が溶ける量の関係を見やすく表したものが溶解度曲線です。見やすくしたグラフのことです。先ほどの関係を溶解度曲線(グラフ)に表してみます。
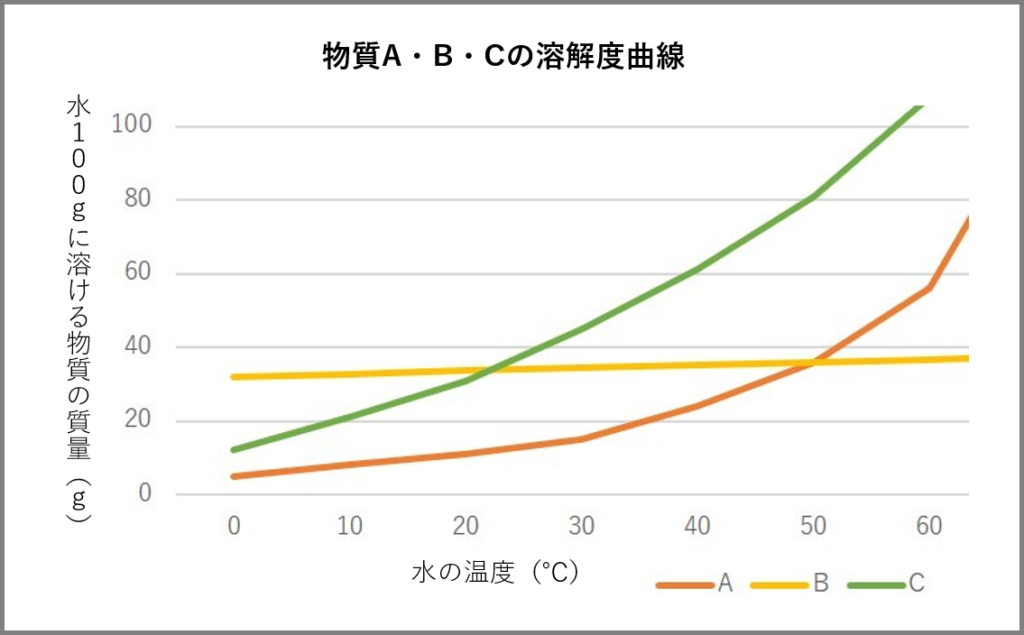
わかりやすいですよね?同じ温度でも溶解度は物質によって全く違うことを覚えておいてください。
水の量が増えた時の考え方
温度以外にもう一つ覚えておくことがあります。それは「水の量」です。
例えば水100gの溶解度が30gの物質があるとします。水200gで同じ物質は何g溶けるか?
答えは60gです。水の量が2倍になったので溶ける物質の量も2倍です。
ただ、この場合に1点気を付けることがあります。先ほどの温度です。同じ水の量でも温度が上がると溶ける物質は増えるので、水が2倍になって温度が同じ温度なら溶ける物質も2倍になる、というのが正しいです。
再結晶とは?
温度を上げると溶解度は増えると説明しましたが、反対に冷やすとどうなると思いますか?
反対なので溶解度は減るが答えです。つまり水に溶けて見えなくなっていた物質が見えるようになります。溶けたままでいられなくなって出てきてしまうんですね。
姿や形が少し変わってしまいますが、この再び表れた物質を取り出すことを「再結晶」といいます。出てきた物質は「結晶」といいます。冷やしたらどれくらいの質量が結晶として取り出せるかをテストで必ず聞かれるので覚えておきましょう。
さあ、問題を解いてみよう
それでは、先ほどの溶解度の表と溶解度曲線をもとに問題を出題します。

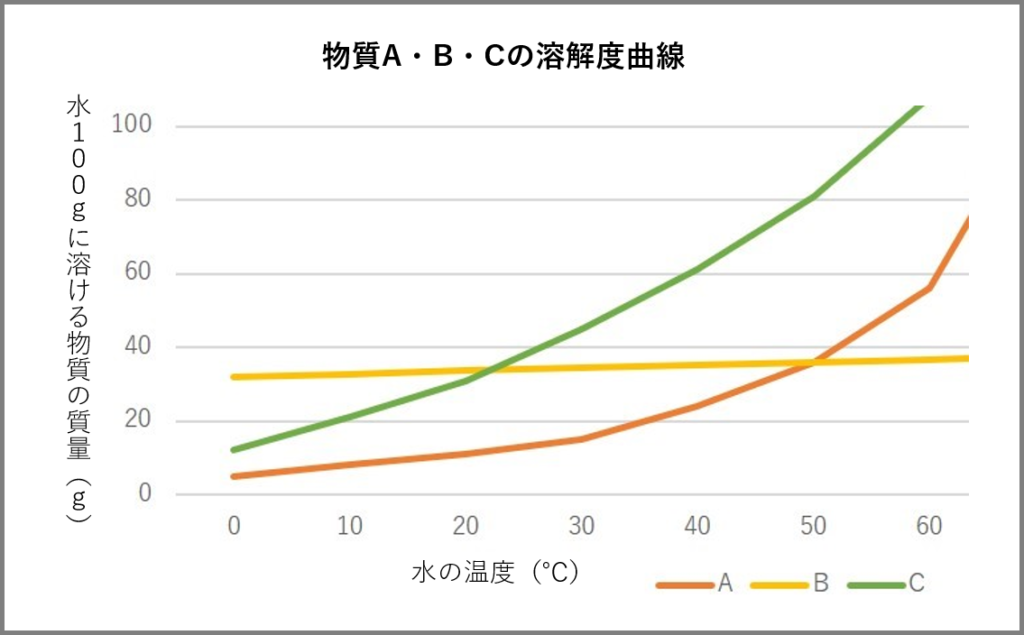
①水100gで温度が30℃の時、一番溶ける質量が多い物質はどれか?
答:物質C
②水100gで温度が40℃の時、物質Aの溶ける質量は何gか?
答:24g
③水200gで温度が20℃の時、物質Bの溶ける質量は何gか?
式:水100gの時の物質Bの溶解度は33.6g → 問題は水200gの溶ける質量と聞かれているから水の量は2倍になるから溶解度も2倍になる 33.6 × 2 = 67.2g
答:67.2g
④温度50℃の水100gに物質A・B・Cそれぞれが溶けていいる飽和水溶液が3つある。この3つの飽和水溶液を全て温度10度まで冷やした時、出てくる結晶の質量が一番多いのはどれか?
式:結晶の質量を物質ごとに計算してみると、物質A 36 – 8 = 28g , 物質B 36 – 32.8 = 3.2g , 物質C 81 – 21 = 60g
答:物質C
⑤温度50℃の水100gに物質Cが溶けている飽和水溶液がある。これを30℃まで冷やしたら物質C
の結晶は何g出てくるか?
式:81 – 45 = 36
答:36g
⑥温度40℃の水300gに物質Aが溶けている飽和水溶液がある。これを20℃まで冷やしたら物質A
の結晶は何g出てくるか?
式:40℃の水300gの物質Aの溶解度は24gの3倍だから 24 × 3 = 72g となる。20℃の水300gの物質Aの溶解度は11gの3倍だから 11 × 3 = 33g となる。よって冷やした時の結晶の質量は 72 – 33 = 39 g となる。
答:39g
まとめ
今回は「溶解度・溶解度曲線」について解説してきました。中学理科の最初の関門である「密度」「濃度」そして今回の「溶解度・溶解度曲線」については計算問題とグラフを読み取る力が重要になります。
問題で聞かれている意味を理解すること、今回出題した問題を確実にクリアできるようになることをお勧めします。きっと得意分野になると思います。ぜひ、高得点目指してください!
中学理科の他ジャンルの解説はこちらから
「密度」の解説
「濃度」の解説








コメント